Задание на лабораторную работу: Создать двоичное дерево поиска, заполняя его числами из файла. Вывести на экран все его листья и неполные вершины, а также их количество.
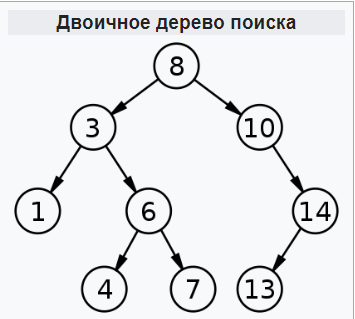
Для начала немного теории для тех кто впервые работает с деревьями. Бинарное или двоичное дерево поиска представлено на рисунке снизу. Для данного рисунка приведем пример. Имеется набор чисел: 8, 3, 6, 10, 1, 14, 4, 7, 13. Необходимо построить бинарное дерево поиска. Объясняя простыми словами, вершиной дерева будет первое число, т.е. 8. Слева от него находятся меньшие числа, справа - бОльшие. Алгоритм построения бинарного дерева таков: вершина дерева 8, далее идет 3; 3 меньше чем 8, пускаем его влево; далее идет 6; 6 меньше чем 8, но больше чем 3; пускаем шестерку вправо от тройки; далее идет 10; 10 больше чем 8; пускаем ее вправо от восьмерки, и т.д.
Листьями в бинарном дереве называют вершины, имеющие степень 0. Говоря простым языком, это те вершины которые "болтаются", не имеют дальнейших связей. Для данного рисунка это вершины: 1, 4, 7 и 13.
Неполными вершинами в бинарном дереве называют вершины у которых только одна дальнейшая (идущая вниз) связь. Для данного рисунка это вершины: 10 и 14.
У бинарного дерева очень много интересных свойств, способов реализаций и прочего, но для данной работы вышеприведенной информации будет достаточно.
Теперь о программе.
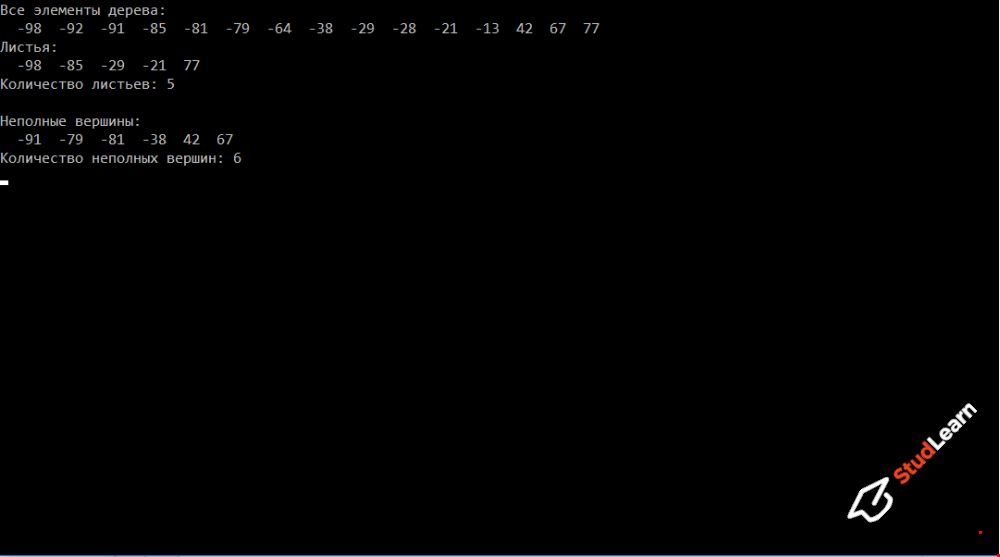
Вначале 15 рандомных чисел от -99 до 99 программно генерируются и записываются в файл, а затем уже из файла считываются в дерево (требование задания). Имеются процедуры, котрые сами за себя говорят: addToTree (добавить число в дерево), printAllElem (вывести все элементы дерева), printLeaf (вывести листья), printNepVer (вывести неполные вершины)).
Приложение:
procedure addToTree(var tree: Ptree; x: Integer);
begin
if tree = nil then
begin
New(tree);
tree.num := x;
tree.left := nil;
tree.right := nil;
end
else
begin
if x < tree.num then
addToTree(tree^.left, x)
else
addToTree(tree^.right, x);
end;
end;
СОДЕРЖАНИЕ АРХИВА:
- Искомый dpr-файл
- Текстовый файл для чисел


 Телеграм
Телеграм

-