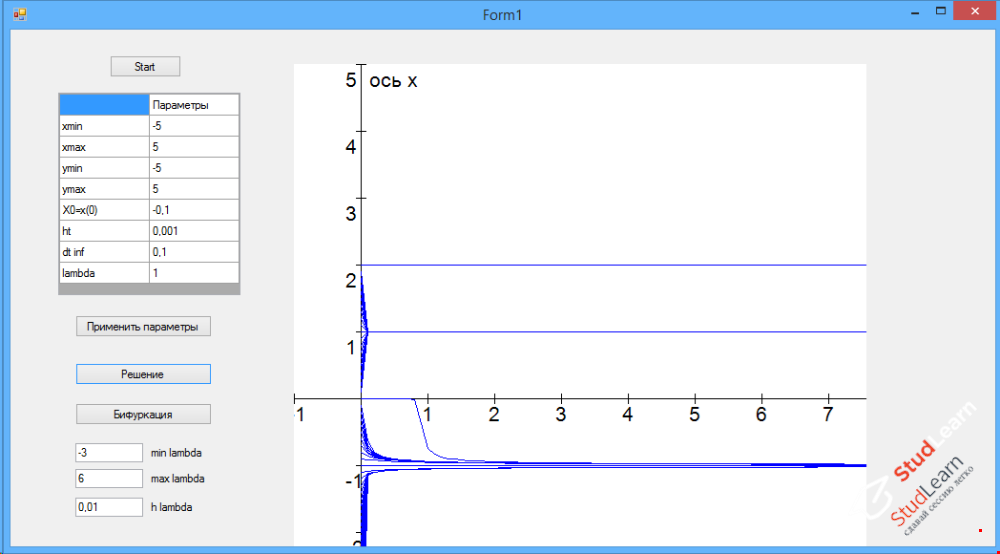
Найти асимптотику решения при начальных значениях в интервале от -5 до 5 с шагом 0.01 и выбранном значении бифуркационного параметра.
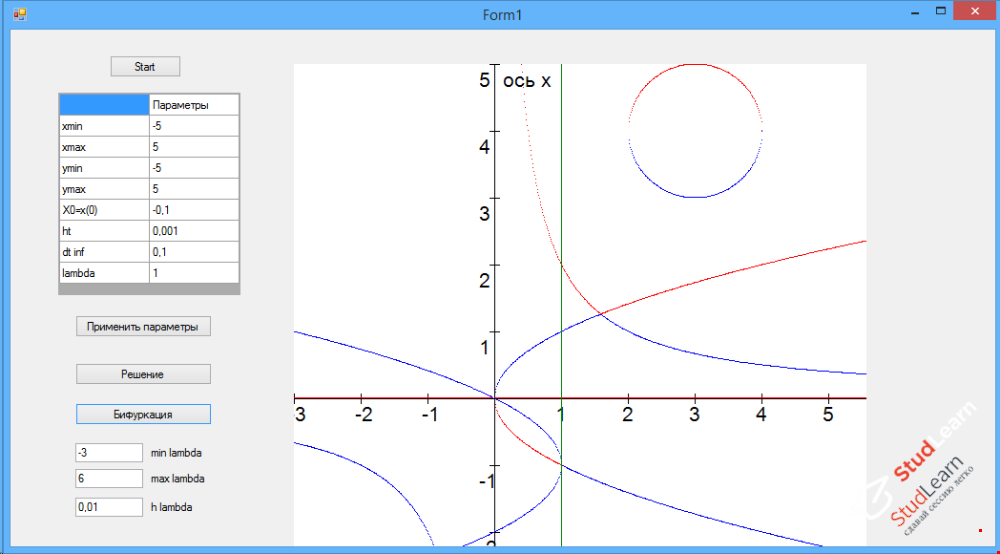
Построить бифуркационную диаграмму. Точки устойчивости обозначить одним цветом, неустойчивости – другим. Привести классификацию точек бифуркации.
Точка бифуркации — критическое состояние системы, при котором система становится неустойчивой относительно флуктуаций и возникает неопределённость: станет ли состояние системы хаотическим или она перейдёт на новый, более дифференцированный и высокий уровень упорядоченности. Термин из теории самоорганизации.
Работа содержит поясниельную записку. Также предоставлен исходный проект на языке С#.
private double func(double lambda1, double x)
{
double F;
F = x * (2 - lambda1 * x) * (lambda1 + 2 * x + Math.Pow(x, 2)) * (Math.Pow(lambda1, 2) + Math.Pow(x, 2) - 6 * lambda1 - 8 * x + 24) * (lambda1 - Math.Pow(x, 2));
return F;
}

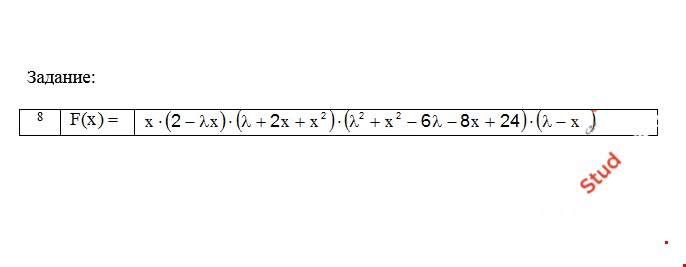
 Телеграм
Телеграм

-