Метод Зейделя Delphi 7

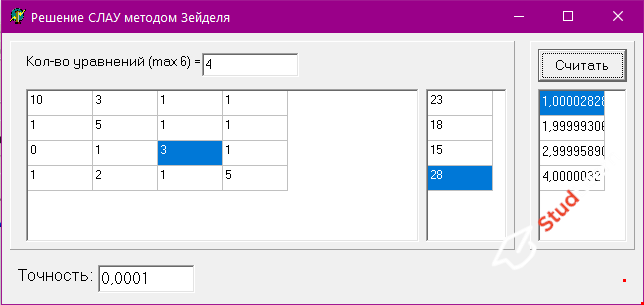
Описание программы

Решение СЛАУ методом Зейделя Идея: задана основная матрица A и вектор B Сначала нормализуем матрицу и вектор. Вычисляется транспонированная матрица A ,т.е A^t; Выполняются действия: A'=(A^t)*A; B'=(A^t)*b Далее операции выполняются над этими матрицами Случайным образом задается вектор X(x1,x2,..,xn); Далее вычисляется вектор Xk через Xk-1.

Фрагмент кода из программы:

procedure TForm1.CalculateClick(Sender: TObject);
var
  i,j,k  : Byte;
  atr : Matrix;
  tt  : Real;
  A1  : Matrix;
  A2  : Matrix;
  B1  : Vector;
  X   : vector;
  X1  : vector;

function CheckConds:Boolean;
{Условие прекращения вычислений}
var
  l : Byte;
  mm : Real;
begin
mm:=abs(X1[1]-X[1]);
for l:=2 to n do begin
if mm<abs(X1[l]-X[l])
  then mm:=abs(X1[l]-X[l]);

  if  mm<eps then CheckConds:=true else CheckConds:=false;
end;

end;

procedure CalculateNextX;
var
  l,m : Byte;
  zz  : real;
begin
for l:=1 to n do begin
  zz:=(B[l]/A[l,l]);
  for m:=1 to n do begin
    if m=l then continue;
    zz:=zz-(A[l,m]*X[m]/A[l,l])
  end;
  X[l]:=zz;
end;
end;

Содержание архива: