Построение выпуклой оболочки для набора точек. Алгоритм Джарвиса. Реализация C#.

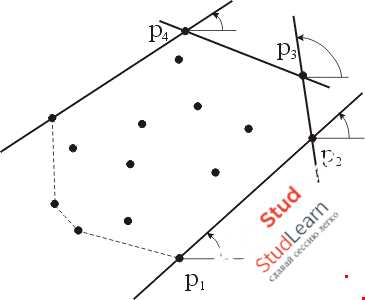
Многоугольник с одинаковым успехом можно задать упорядоченным множеством как его ребер, так и его вершин. В задаче о выпуклой оболочке мы до сих пор обращали внимание главным образом на изолированные крайние точки. А что если вместо этого попытаться определить ребра выпуклой оболочки, приведет ли такой подход к созданию практически пригодного алгоритма? Если задано множество точек, то довольно трудно быстро определить, является или нет некоторая точка крайней. Однако если даны две точки, то непосредственно можно проверить, является или нет соединяющий их отрезок ребром выпуклой оболочки.

Теорема. Отрезок l, определяемый двумя точками, является ребром выпуклой оболочки тогда и только тогда, когда все другие точки заданного множества лежат на l или с одной стороны от него.

Джарвис использовал эту идею, и в этом разделе мы рассмотрим предложенный им алгоритм.