Вычисление экстремумов функций с помощью градиентного метода C#

Задание по работе:

• Изучить теоретическую часть работы.
• Реализовать метод градиентного спуска
• Для функций двух видов: вогнутой и с вторичными минимумами применить реализованный метод, оценить скорость сходимости и возможность нахождения глобального минимума.

Содержание

//В примере указан метод для функции синусов
    {
        const int u = 100000;
        // функция 1
        public static double Func(double x)
        {
            return Math.Sin(x) + Math.Sin(x * x);
        }

        // производная функции 1
        public static double Proizv1(double x)
        {
            return Math.Cos(x) + 2 * x * Math.Cos(x * x);
        }
        // Х1 для функции 1 
        public static double x1(double x, double a)
        {
            return x - a * Proizv1(x)/Math.Abs(Proizv1(x));
        }

Содержание архива 

• Исходный код на C# Windows Forms для Visual Studio

Пояснение к программе

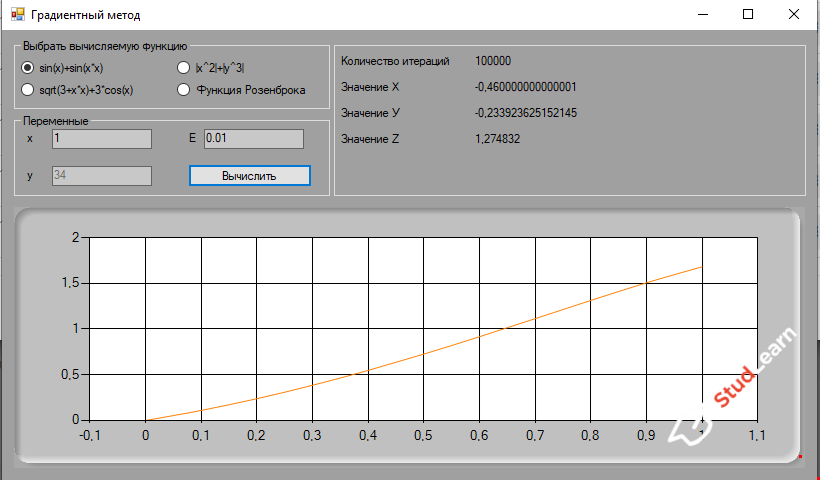
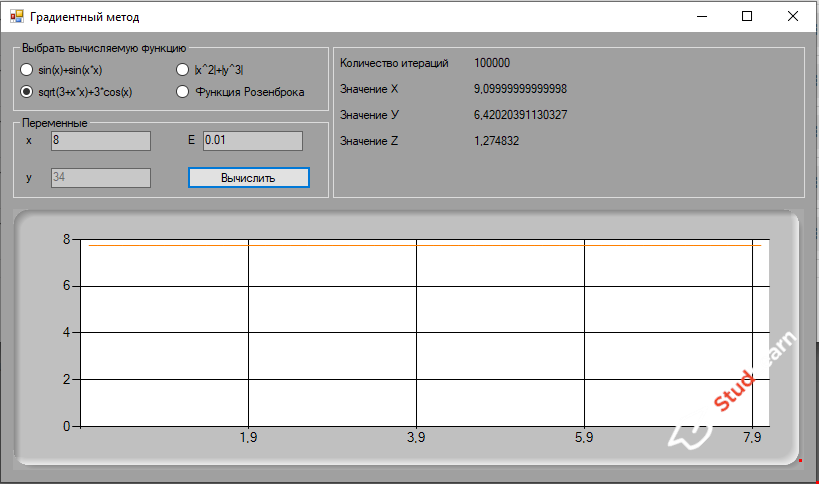
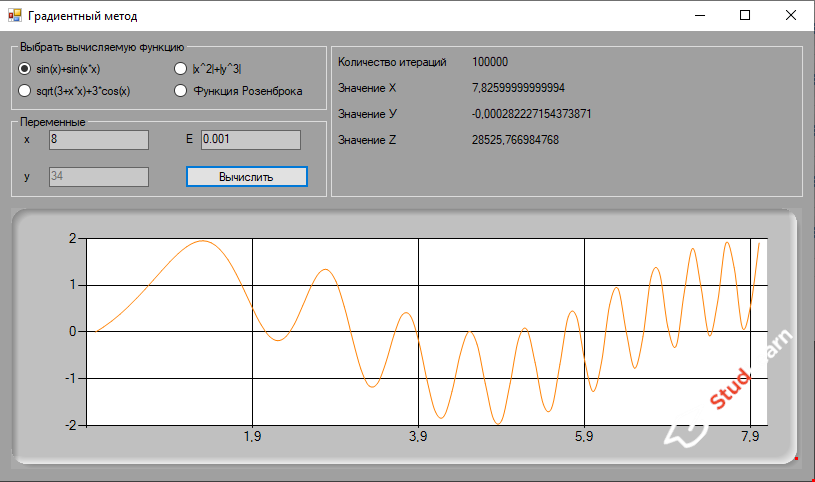
В двух последних функциях на графике отображается точка, так как это трехмерные функции и экстремумы показываются на двумерной проекции трехмерного графика.